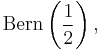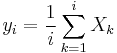Optimal stopping
In mathematics, the theory of optimal stopping is concerned with the problem of choosing a time to take a particular action, in order to maximise an expected reward or minimise an expected cost. Optimal stopping problems can be found in areas of statistics, economics, and mathematical finance (related to the pricing of American options). A key example of an optimal stopping problem is the secretary problem. Optimal stopping problems can often be written in the form of a Bellman equation, and are therefore often solved using dynamic programming.
Contents |
Definition
Stopping rule problems are associated with two objects:
- A sequence of random variables
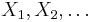 , whose joint distribution is something assumed to be known
, whose joint distribution is something assumed to be known - A sequence of 'reward' functions
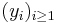 which depend on the observed values of the random variables in 1.:
which depend on the observed values of the random variables in 1.:
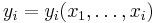
Given those objects, the problem is as follows:
- You are observing the sequence of random variables, and at each step
 , you can choose to either stop observing or continue
, you can choose to either stop observing or continue - If you stop observing at step
 , you will receive reward
, you will receive reward 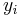
- You want to choose a stopping rule to maximise your expected reward (or equivalently, minimise your expected loss)
Examples
Coin tossing ( converges)
converges)
You have a fair coin and are repeatedly tossing it. Each time, before it is tossed, you can choose to stop tossing it and get paid (in dollars, say) the average number of heads observed.
You wish to maximise the amount you get paid by choosing a stopping rule. If Xi (for i ≥ 1) forms a sequence of independent, identically distributed random variables with distribution
and if
then the sequences 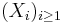 , and
, and 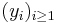 are the objects associated with this problem.
are the objects associated with this problem.
House selling (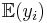 does not necessarily converge)
does not necessarily converge)
You have a house and wish to sell it. Each day you are offered 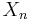 for your house, and pay
for your house, and pay  to continue advertising it. If you sell your house on day
to continue advertising it. If you sell your house on day  , you will earn
, you will earn 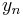 , where
, where 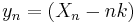 .
.
You wish to maximise the amount you earn by choosing a stopping rule.
In this example, the sequence (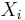 ) is the sequence of offers for your house, and the sequence of reward functions is how much you will earn.
) is the sequence of offers for your house, and the sequence of reward functions is how much you will earn.
Secretary problem (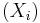 is a finite sequence)
is a finite sequence)
You are observing a sequence of objects which can be ranked from best to worst. You wish to choose a stopping rule which maximises your chance of picking the best object.
Here, if  (n is some large number, perhaps) are the ranks of the objects, and
(n is some large number, perhaps) are the ranks of the objects, and 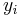 is the chance you pick the best object if you stop intentionally rejecting objects at step i, then
is the chance you pick the best object if you stop intentionally rejecting objects at step i, then 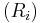 and
and 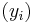 are the sequences associated with this problem. This problem was solved in the early 1960s by several people. An elegant solution to the secretary problem and several modifications of this problem is provided by the more recent odds algorithm of optimal stopping (Bruss algorithm).
are the sequences associated with this problem. This problem was solved in the early 1960s by several people. An elegant solution to the secretary problem and several modifications of this problem is provided by the more recent odds algorithm of optimal stopping (Bruss algorithm).
Search theory
Economists have studied a number of optimal stopping problems similar to the 'secretary problem', and typically call this type of analysis 'search theory'. Search theory has especially focused on a worker's search for a high-wage job, or a consumer's search for a low-priced good.
References
- T. P. Hill. "Knowing When to Stop". American Scientist, Vol. 97, 126-133 (2009). (For French translation, see cover story in the July issue of Pour la Science (2009))
- Optimal Stopping and Applications, retrieved on 21 June 2007
- Thomas S. Ferguson. "Who solved the secretary problem?" Statistical Science, Vol. 4.,282-296, (1989)
- F. Thomas Bruss. "Sum the odds to one and stop." Annals of Probability, Vol. 28, 1384–1391,(2000)
- F. Thomas Bruss. "The art of a right decision: Why decision makers want to know the odds-algorithm." Newsletter of the European Mathematical Society, Issue 62, 14-20, (2006)
- R. Rogerson, R. Shimer, and R. Wright (2005), 'Search-theoretic models of the labor market: a survey'. Journal of Economic Literature 43, pp. 959–88.